桑原 知剛
量子複雑性解析理研白眉研究チーム 理研白眉チームリーダー
研究概要
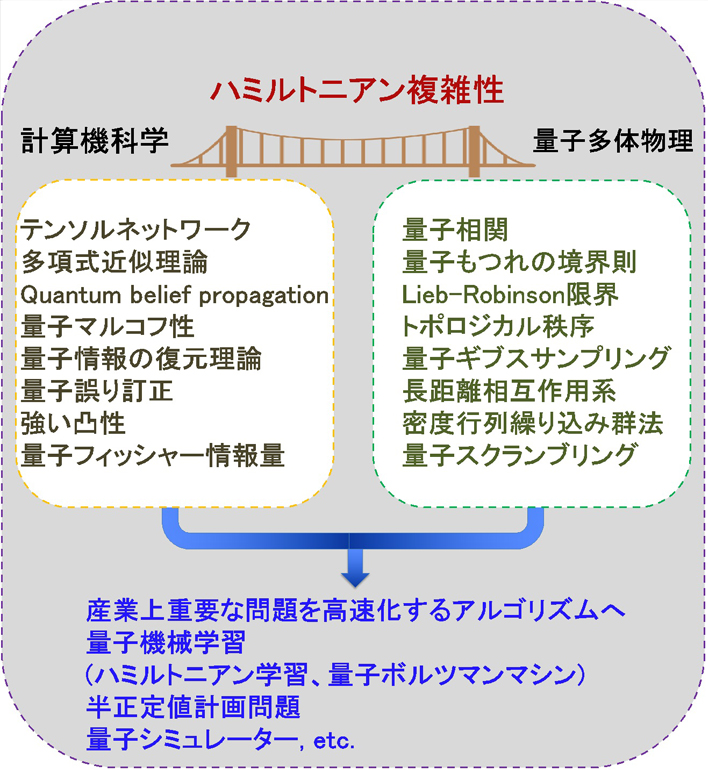
古典コンピュータ(または量子コンピュータ)を用いたときに、量子多体系のシミュレーションの計算複雑性を明らかにする分野はハミルトニアン複雑性(Hamiltonian Complexity)と呼ばれています。とりわけ、近年の量子コンピュータの量子超越性やNISQ(誤り訂正機能のない小型の量子コンピュータ)を用いた量子アルゴリズムの観点から、ハミルトニアン複雑性は量子情報分野において最も重要な研究対象の一つとなっています。本研究では、ハミルトニアン複雑性における数学的な未解決問題を解決していくことを目指しています。
主な研究テーマ
・量子もつれの境界則の研究
・相互作用するボソン系におけるLieb-Robinson限界の研究
・任意の温度における量子マルコフ性の研究
代表的な研究成果
・T. Kuwahara, K. Saito, “Strictly Linear Light Cones in Long-Range Interacting Systems of Arbitrary Dimensions,”
Physical Review X, 10, 031010 (2020), Featured in Physics
理研プレスリリース:線形光円錐問題の数学的な解決
・T. Kuwahara, K. Saito, “Area law of noncritical ground states in 1D long-range interacting systems,” Nature Communications, 11 4478 (2020)
理研プレスリリース:量子もつれの境界則に対する新しいメカニズムの発見
・T. Kuwahara, A. M. Alhambra, and A. Anshu, “Improved thermal area law and quasi-linear time algorithm for quantum Gibbs states,” Physical Review X, 11, 11047 (2021)
理研プレスリリース:低温下における量子もつれの新法則を発見
・A. Anshu, S. Arunachalam, T. Kuwahara, M. Soreimanifar (alphabet order), “Sample-efficient learning of quantum many-body systems,” Nature Physics, 17, 931–935 (2021), Featured in News&Views
理研プレスリリース: “自然界”を効率的に学習する方法を開発
・T. Minato, K. Sugimoto, T. Kuwahara, “Fate of measurement-induced phase transition in long-range interactions ,” K. Saito, Physical Review Letters 128, 010603 (2022), Editor’ suggestion, Featured in Physics
理研プレスリリース:量子もつれに劇的な変化をもたらす新たな条件の発見
・T. Kuwahara, K. Saito, “Exponential Clustering of Bipartite Quantum Entanglement at Arbitrary Temperatures,” To appear in Physical Review X