
Bartosz Regula
RIKEN Hakubi Team Leader,
Mathematical Quantum Information RIKEN Hakubi Research Team
Outline
Our group studies the mathematical underpinnings of quantum information theory, with a particular focus on the investigation of the mathematical structure of quantum resources — physical phenomena that underlie practical advantages of quantum technologies in areas such as communication and computation.We aim to develop technical frameworks that help address the fundamental questions of how to quantify, manipulate, and take advantage of physical resources in quantum information and communication tasks. Our approach is to establish a solid and rigorous mathematical foundation which can be directly used to study a variety of physical settings, allowing for broad applications and generalisations.
Representative Research Results
・ L. Lami and B. Regula, “No second law of entanglement manipulation after all”, Nat. Phys. 19, 184–189 (2023)
・ B. Regula, “Probabilistic transformations of quantum resources”, Phys. Rev. Lett. 128, 110505 (2022)
・ B. Regula and R. Takagi, “Fundamental limitations on distillation of quantum channel resources”, Nat. Commun. 12, 4411 (2021)
・ J. R. Seddon, B. Regula, H. Pashayan, Y. Ouyang, and E. T. Campbell, “Quantifying quantum speedups: improved classical simulation from tighter magic monotones”, PRX Quantum 2, 010345 (2021)
・ R. Takagi and B. Regula, “General resource theories in quantum mechanics and beyond: operational characterization via discrimination tasks”, Phys. Rev. X 9, 031053 (2019)
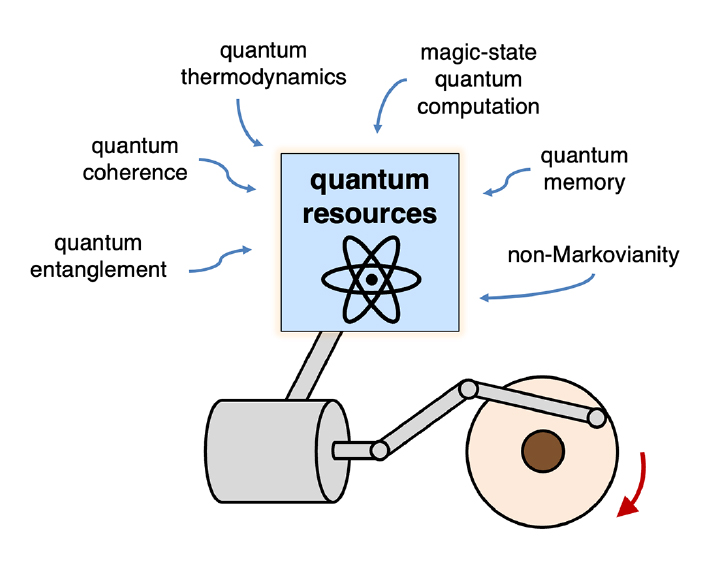
There are many different quantum resources that can fuel the practical applications of quantum technologies. Understanding their properties is thus an important problem, but their complex mathematical structure often makes this very difficult. (Schematic figure adapted from Phys. Rev. X 9, 031053 (2019).)